Distribusi Binomial

Sering dalam berbagai macam permasalahan peluang hanya memiliki dua kemungkinan hasil atau dapat disederhanakan menjadi dua kemungkinan. Sebagai contoh, ketika suatu koin dilempar, maka kita akan mendapat angka atau gambar. Ketika seorang bayi lahir, maka seorang bayi tersebut merupakan bayi laki-laki atau perempuan. Dalam permainan bola basket, tim yang bermain bisa menang atau kalah. Keadaan benar/salah tersebut dapat dijawab dengan dua cara, yaitu benar atau salah. Kondisi-kondisi lainnya dapat disederhanakan untuk menghasilkan dua kemungkinan. Sebagai contoh, suatu pengobatan medis dapat diklasifikasikan sebagai efektif atau tidak efektif, tergantung hasilnya. Seseorang dapat dikategorikan memiliki tekanan darah normal atau tidak normal, tergantung dari pengukuran tekanan darahnya. Pertanyaan-pertanyaan pilihan ganda, walaupun memiliki empat atau lima pilihan jawaban, dapat diklasifikasikan menjadi benar atau salah. Kondisi-kondisi yang telah dicontohkan tersebut dinamakan percobaan binomial.

Pada pembahasan ini kita akan membahas beberapa hal mengenai distribusi binomial, yaitu:

• Percobaan binomial.
• Pengertian distribusi binomial.
• Rumus peluang binomial.
• Menghitung peluang binomial dengan tabel.
• Rata-rata, varians, dan simpangan baku untuk distribusi binomial.

---

Percobaan binomial merupakan suatu percobaan yang memenuhi empat syarat berikut:

1. Terdapat n kali percobaan.
2. Masing-masing percobaan hanya dapat menghasilkan dua kemungkinan, atau hasil yang diperoleh dapat disederhanakan menjadi dua kemungkinan. Hasil yang diperoleh tersebut dapat dianggap sebagai hasil yang sukses atau gagal.
3. Hasil dari masing-masing percobaan haruslah saling bebas.
4. Peluang untuk sukses harus sama untuk setiap percobaan.

---

Suatu percobaan binomial dan hasilnya memberikan distribusi peluang khusus yang disebut sebagai distribusi binomial.

Hasil-hasil percobaan binomial dan peluang yang bersesuaian dari hasil tersebut dinamakan distribusi binomial.

Dalam percobaan binomial, hasil-hasilnya seringkali diklasifikasikan sebagai hasil yang sukses atau gagal. Sebagai contoh, jawaban benar suatu pertanyaan pilihan ganda dapat diklasifikasikan sebagai hasil yang sukses, sehingga pilihan jawaban lainnya merupakan jawaban yang salah dan diklasifikasikan sebagai hasil yang gagal. Notasi-notasi yang umumnya digunakan dalam percobaan binomial dan distribusi binomial adalah sebagai berikut.

Notasi	Keterangan
P(S)	Simbol untuk peluang sukses.
P(F)	Simbol untuk peluang gagal.
p	Peluang sukes.
q	Peluang gagal.
	P(S) = p dan P(F) = 1 – p = q
n	Banyaknya percobaan
X	Banyaknya sukses dalam n kali percobaan
Perhatikan bahwa 0 ≤ X ≤ n dan X = 0, 1, 2, 3, …, n.

Peluang sukses dalam percobaan binomial dapat dihitung dengan menggunakan rumus berikut.

---

Rumus Peluang Binomial

Dalam suatu percobaan binomial, peluang untuk mendapatkan tepat X sukses dalam npercobaan adalah

---

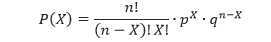
Untuk mengetahui bagaimana ilustrasi dari rumus peluang binomial tersebut bermula, perhatikan Contoh 1 berikut.

Contoh 1: Melempar Koin

Suatu koin dilempar sebanyak tiga kali. Tentukan peluang mendapatkan tepat dua angka.

Pembahasan Permasalahan ini dapat diselesaikan dengan melihat ruang sampelnya. Ruang sampel dari pelemparan satu koin sebanyak tiga kali adalah

S = {AAA, AAG, AGA, GAA, GGA, GAG, AGG, GGG}

Dari ruang sampel, kita dapat melihat bahwa ada tiga cara untuk mendapatkan tepat dua angka, yaitu AAG, AGA, dan GAA. Sehingga peluang kita mendapatkan tepat dua angka adalah 3/8 atau 0,375.

Dengan melihat kembali Contoh 1 dari sudut pandang percobaan binomial, maka contoh tersebut memenuhi keempat kriteria percobaan binomial.

1. Terdapat tiga kali percobaan.
2. Setiap percobaan hanya memiliki dua kemungkinan, yaitu angka (A) atau gambar (G).
3. Hasil dari masing-masing percobaan saling bebas (hasil dari suatu pelemparan tidak mempengaruhi hasil pelemparan lainnya).
4. Peluang percobaan sukses (angka) adalah ½ di setiap percobaannya.

Dalam kasus ini, n = 3, X = 2, p = ½, dan q = ½. Sehingga dengan mensubstitusi nilai-nilai tersebut ke dalam rumus, kita mendapatkan

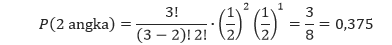
Jawaban tersebut sama dengan jawaban kita sebelumnya yang menggunakan ruang sampel.

Contoh 1 tersebut juga dapat digunakan untuk menjelaskan rumus peluang binomial. Pertama, perhatikan bahwa terdapat tiga cara untuk mendapatkan tepat dua angka dan satu gambar dari delapan kemungkinan. Ketiga cara tersebut adalah AAG, AGA, dan GAA. Sehingga, dalam kasus ini banyaknya cara kita mendapatkan dua angka dari pelemparan koin sebanyak tiga kali adalah 3C2, atau 3. Secara umum, banyak cara untuk mendapatkanX sukses dari n percobaan tanpa memperhitungkan urutannya adalah

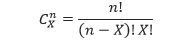
Ini merupakan bagian pertama rumus binomial. (Beberapa kalkulator dapat digunakan untuk menghitung kombinasi tersebut).

Selanjutnya, masing-masing sukses memiliki peluang ½ dan muncul sebanyak dua kali. Demikian juga masing-masing gagal memiliki peluang ½ dan muncul sekali. Sehingga akan memberikan,

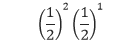
pada rumus binomial. Sehingga apabila masing-masing percobaan sukses sukses memiliki peluang p dan muncul X kali serta peluang gagalnya adalah q dan muncul n – X kali, maka dengan menuliskan peluang percobaan sukses kita akan mendapatkan rumus binomial.

Semoga Bermanfaat ;)